Conceptos
¿QUÉ ES LA ESTADÍSTICA?
APLICACIONES DE LA
ESTADÍSTICA
La estadística tiene una amplia gama de aplicaciones en diversos campos.
1. Investigación científica: En ciencia, la estadística se utiliza para diseñar experimentos, analizar datos y sacar conclusiones significativas. Ayuda a los científicos a validar hipótesis y entender la variabilidad en los resultados.
2. Economía y negocios: En economía, la estadística se usa para el análisis de mercados, la predicción económica, la evaluación de riesgos financieros y la toma de decisiones empresariales basadas en datos.
3. Medicina y ciencias de la salud: En medicina, la estadística es esencial para la investigación clínica, los ensayos clínicos, el análisis epidemiológico y la evaluación de tratamientos médicos basados en evidencia.
4. Ingeniería y tecnología: En ingeniería, la estadística se utiliza para el control de calidad, la confiabilidad de sistemas y productos, y la optimización de procesos industriales.
5. Ciencias sociales: En disciplinas como la psicología, la sociología y la ciencia política, la estadística se aplica para estudiar comportamientos humanos, patrones sociales, encuestas de opinión y estudios de mercado.
6. Educación: En educación, la estadística se usa para evaluar el rendimiento estudiantil, diseñar pruebas y evaluar la efectividad de métodos educativos.
7. Medio ambiente: En ciencias ambientales, la estadística es crucial para el análisis de datos climáticos, la evaluación de impactos ambientales y la gestión de recursos naturales.
8. Investigación de mercados: En marketing, la estadística se emplea para analizar datos de consumidores, segmentar mercados y predecir tendencias de compra.
En resumen, la estadística proporciona herramientas para recolectar, analizar e interpretar datos en una amplia variedad de disciplinas, contribuyendo así al avance del conocimiento y la toma de decisiones fundamentadas en evidencia empírica.
DATO ESTADÍSTICO
Un dato estadístico es una pieza individual de información recolectada y registrada para su análisis en el contexto de un estudio estadístico. Este dato puede ser numérico o categórico y representa una observación o medición de alguna característica de un sujeto, objeto, evento o fenómeno.
TIPOS DE ESTADÍSTICA
1. ESTADÍSTICA DESCRIPTIVA
La estadística descriptiva se encarga de recolectar, organizar, presentar y describir un conjunto de datos con el fin de resumir sus características principales de manera sencilla y comprensible. Utiliza tablas, gráficos y medidas estadísticas para proporcionar una visión clara y concisa de los datos.
Técnicas y Herramientas
1. Tablas de frecuencias: Organiza los datos en categorías y muestra la frecuencia con la que aparece cada categoría.
2. Gráficos: Como histogramas, diagramas de barras, diagramas de sectores (pastel), diagramas de dispersión, etc.
3. Medidas de tendencia central: Como la media, la mediana y la moda.
4. Medidas de dispersión: Como la variación, la desviación estándar, el rango y el coeficiente de variación.
5. Medidas de posición: Como los percentiles, deciles y cuartiles.
2. ESTADÍSTICA INFERENCIAL
La estadística inferencial se utiliza para hacer generalizaciones o inferencias sobre una población a partir de una muestra de datos. Se basa en la teoría de probabilidades y utiliza muestras para hacer estimaciones y tomar decisiones.
Técnicas y Herramientas
1. Estimación: Punto y por intervalo (intervalos de confianza) para estimar parámetros poblacionales.
2. Pruebas de hipótesis: Para contrastar afirmaciones o hipótesis sobre una población.
3. Análisis de regresión: Para investigar y modelar relaciones entre variables.
4. Análisis de varianza (ANOVA): Para comparar las medias de tres o más grupos.
5. Modelos de probabilidad: Para describir y predecir comportamientos y resultados aleatorios.
El análisis estadístico implica la recolección, descripción, presentación y análisis de los datos, por medio de métodos gráficos (diagramas) que permiten estudiar y fácil interpretar, proporcionar pistas valiosas desde el punto de vista analítico.
Los gráficos se clasifican en: gráficos de tendencia y circular. Pueden ser
muestra a un número determinado de sujetos, pero es común presentar la información a la población de clientes potenciales en su conjunto.
TIPOS DE VARIABLES
En estadística, las variables son características o atributos que pueden tomar diferentes valores. Se clasifican principalmente en dos grandes categorías: cualitativas (categóricas) y cuantitativas (numéricas). A continuación, se describen en detalle los tipos de variables:
VARIABLES CUALITATIVAS (CATEGORÍAS)
Son aquellas que describen cualidades o características y no tienen un valor numérico intrínseco.
1. VARIABLES NOMINALES:
Descripción: No tienen un orden o jerarquía. Simplemente etiquetan categorías. Ejemplos:
2. VARIABLES ORDINALES:
Descripción: Tienen un orden o jerarquía natural, pero las diferencias entre los valores no son numéricamente significativas. Ejemplos:
VARIABLES CUANTITATIVAS (NUMÉRICAS)
1. MEDIOS ARITMÉTICOS
La media aritmética o promedio de un conjunto de datos es el valor obtenido al sumar todos ellos y dividir el resultado entre el número total de datos.
La forma de calcular o calcularse podría ser: Sumar todos los datos y luego se divide entre el número de datos n. Ahora bien, si pensamos en la fórmula general de la media aritmética, esta sería: Donde: Σ: Suma de cada x: Cada dato n: Número total de datos del conjunto Gracias al símbolo Σ podemos acortar la fórmula general para la media aritmética.
2. MODA
¿Qué es la moda en estadística? La moda es el valor que más se repite en un conjunto de datos o el intervalo de clase que concentra la mayor frecuencia. Si los datos se agrupan en clases específicas, podríamos hablar de una clase modal.
Ejemplo: Vamos a calcular la moda con los datos del primer ejemplo que teníamos y con la siguiente distribución de probabilidad. a) Con los datos: 20, 19, 20, 40, 50. Calculamos las diferentes frecuencias: 20 se repite 2 veces (f = 2); 19 se repite 1 vez (f = 1); 40 se repite 1 vez; 50 se repite 1 vez. Por tanto, la moda vale 20, puesto que es el valor que más veces se repite.
3. MEDIANA
La mediana es el número que, cuando ordenas a todos en orden de menor a mayor ingreso, deja la mitad de ellos con un ingreso inferior y la otra mitad con uno superior; Al ser una medida relativa, su valor varía dependiendo del nivel de ingresos y de cómo se distribuye entre la población.
Por ejemplo, la mediana de 2, 3, 3, 5, 7 y 10 es 4.
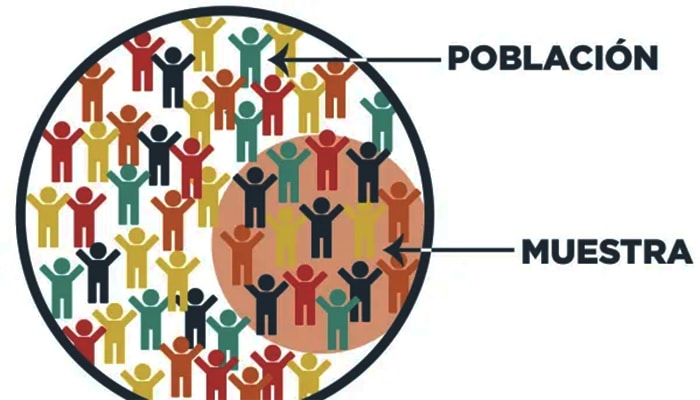
4. POBLACIÓN
Es un conjunto de elementos o eventos similares que son de interés para alguna pregunta o experimento.
Con características en común, determinadas, observables y medibles.
5. MUESTRA
Es un subconjunto representativo de una población que se estudia con el propósito de obtener información sobre esa población , es decir se trata de un fragmento de la totalidad de elementos a estudiar, dichas muestras se obtienen a través de diferentes técnicas estadísticas que garantizan distintos mecanismos.
DESVIACIÓN TÍPICA O ESTÁNDAR
La desviación estándar es una medida estadística que cuantifica la cantidad de variación o dispersión de un conjunto de datos. Es una herramienta crucial en estadística, ya que indica qué tan dispersos están los valores de los datos en relación con la media del conjunto de datos. A continuación, se detalla cómo se define y cómo se calcula la desviación estándar.
Definición
La desviación estándar se denota combinada por la letra griega sigma ( ) cuando se refiere a una población, y por la letra
cuando se refiere a una muestra. Una desviación estándar baja indica que los datos tienden a estar cerca de los medios, mientras que una desviación estándar alta indica que los datos están más dispersos.
¿QUÉ ES LA VARIANZA?
La varianza es una medida de dispersión que representa la variabilidad de una serie de datos respecto a su medio.
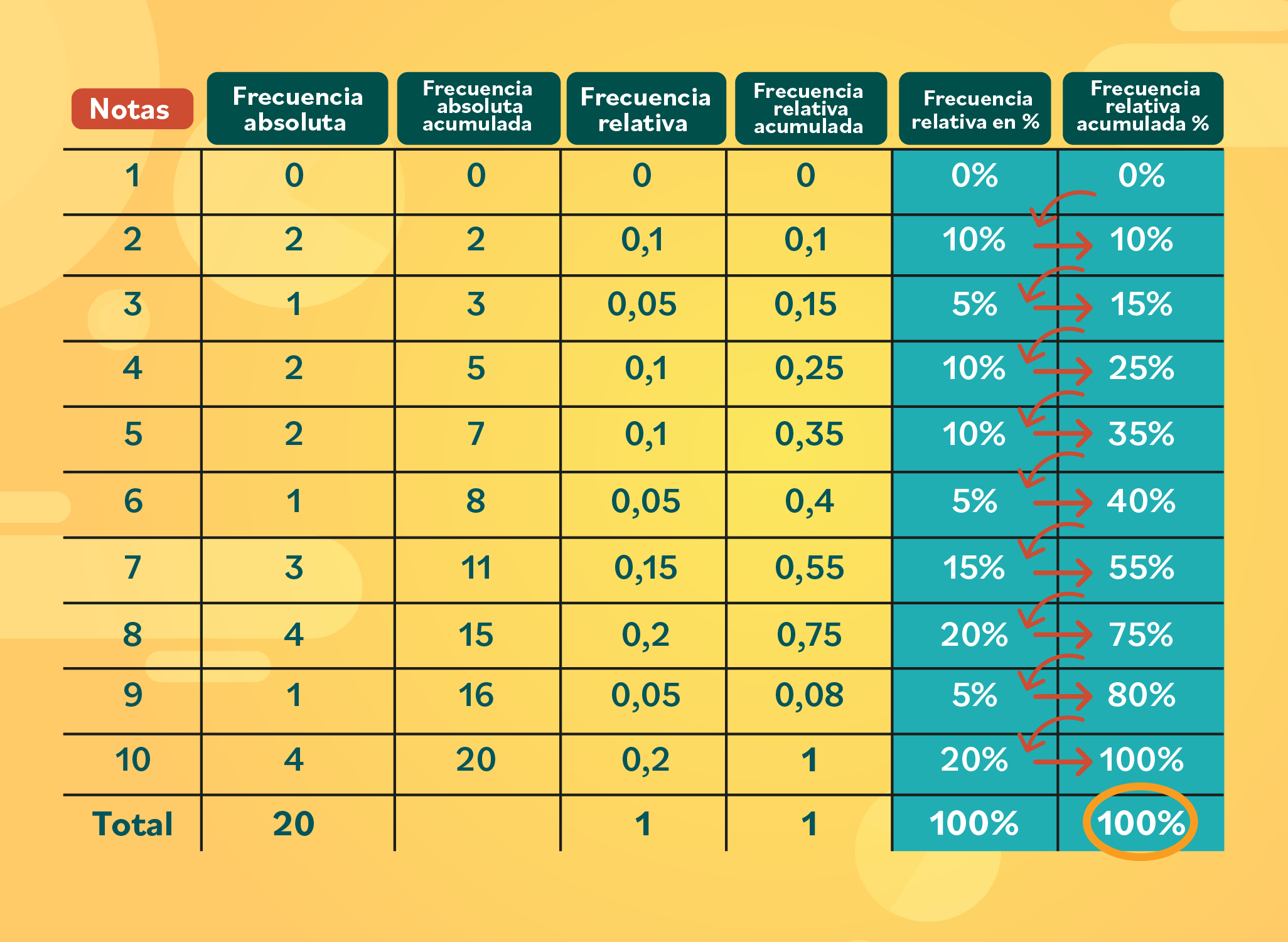
TABLA DE FRECUENCIAS
Una tabla de frecuencias es una herramienta utilizada en estadística para organizar y resumir un conjunto de datos, en ésta se muestra la frecuencia (el número de veces) que cada valor o rango de valores aparece en el conjunto de datos.
La tabla de frecuencias puede incluir frecuencias absolutas, relativas, acumuladas y acumuladas relativas.
Para la elaboración de una tabla de frecuencias se deben seguir ciertos pasos:
1. Recolectar los datos: reúne el conjunto de datos que deseas analizar.
2. Determinar los valores únicos: identificar los valores únicos (o clases, si los datos son continuos) en el conjunto de datos.
3. Contar las frecuencias: cuenta cuantas veces aparece cada valor único en el conjunto de datos.
4. Calcular frecuencias adicionales: si es necesario, calcule las frecuencias relativas, acumuladas y acumuladas relativas.
TIPOS DE FRECUENCIAS
Frecuencia absoluta (f): el número de veces que un valor específico aparece en el conjunto de datos. Esta frecuencia se puede representar indicando entre paréntesis el valor xy su respectiva frecuencia f. Ejemplo: (xf). La frecuencia absoluta (f). Este valor propagado en el intervalo en que se distribuyen los valores de un conjunto de datos se obtiene sumando la frecuencia de un ciclo completo. Si por el contrario los datos están codificados en un contexto de intervalo se consideran.
Frecuencia relativa (fr): la proporción o porcentaje que representa la frecuencia absoluta en relación con el total de datos. Se calcula dividiendo la frecuencia absoluta por el total de observaciones. La relativa (F). Es un dato diseñado de acuerdo a un esquema proporcional o base de datos de manera que se obtiene mediante la ecuación: (1) F = (f) n ó (2) = xn = i 1. i xi Xi n donde F = frecuencia relativo; f = frecuencia absoluta; x = valor de la variable de interés; n = número de datos del conjunto, dato o casos.
frecuencia absoluta
Frecuencia relativa = ----------------------------
Total de observaciones
Frecuencia acumulada (F): la frecuencia acumulada es una medida estadística que muestra el número total de observaciones que se encuentran por debajo de un valor específico en un conjunto de datos. Es la suma de las frecuencias absolutas de todos los valores anteriores y el valor en cuestión. La frecuencia acumulada ayuda a entender la distribución de los datos ya identificar la posición relativa de los valores dentro del conjunto de datos.
Frecuencia relativa acumulada (Fr): es una medida estadística que muestra la proporción acumulada de observaciones hasta un determinado valor en un conjunto de datos. Se calcula sumando las frecuencias relativas de todos los valores anteriores y el valor actual. La frecuencia relativa acumulada es útil para entender la distribución de los datos y para identificar percentiles y otros estadísticos descriptivos.
Te comparto el siguiente video para reforzar mi punto de vista:
BIBLIOGRAFÍA
Carreón, D. (22 de febrero de 2021). Tabla de frecuencias súper fácil - Para principiantes. [Video]. YoTuBe.
CGF GLOBAL. (17 de julio de 2022). ¿Qué es una tabla de frecuencias?
Ferrer, C., Almeida, F., Escalada, L., Gispert, I. (2005). Educación estadística para el desarrollo profesional de los docentes. Revista Latinoamericana de Investigación en Matemática Educativa, 8, 73-96.
García, S., Martínez, J. (2002). Conceptos de media aritmética, moda y mediana en Estadística. Cómo tratarlos en Educación Secundaria. Enseñanza de las Ciencias, XX Nº 3, 455-465.
.png)





Comments